自然现象和社会现象中许多要解决的问题所归结的数学模型中,大量的是含有两个或更多个独立变量的函数的微分方程,即偏微分方程。
偏微分方程可按它与时间有关与否分成两类。如一个物体内热量的稳态分布,在数学上可用第三章中的 Laplace 方程来刻画,它与时间没有关系,我们称其为定常的。
但是更多的是一类与时间有关,即不定常的方程。求解这类问题就是要找到方程所描述的系统的状态随时间的变化而变化的规律,进而根据该系统在某个 t 0 t_{0} t 0 t t t t 0 t_{0} t 0
用解析方法求解发展方程,并通过已知函数把解表示出来,这只有在极个别情况下才能做到,绝大多数情况都是要靠数值方法来追踪的。本章将讨论发展方程——主要是热传导方程和波动方程的差分方法。由于所考虑系统的状态量不仅与时间 t t t x x x y y y z , ⋯ z, \cdots z , ⋯
扩散方程
假定有一根单位长度的细竿,当 t = 0 t=0 t = 0 x x x φ ( x ) \varphi(x) φ ( x ) φ ( 0 ) = φ ( 1 ) = 0 \varphi(0)=\varphi(1)=0 φ ( 0 ) = φ ( 1 ) = 0 t t t u ( x , t ) u(x,t) u ( x , t )
{ ∂ u ∂ t = a ∂ 2 u ∂ x 2 ( a > 0 ) , 0 < t ⩽ T , 0 < x < 1 , ( 5.1 ) u ( 0 , t ) = u ( 1 , t ) = 0 , t > 0 , ( 5.2 ) u ( x , 0 ) = φ ( x ) , 0 ⩽ x ⩽ 1 , ( 5.3 ) \left\{\begin{array}{l}
\frac{\partial u}{\partial t}=a \frac{\partial^{2} u}{\partial x^{2}} \quad(a>0), 0<t \leqslant T, 0<x<1, (5.1) \\
u(0, t)=u(1, t)=0, \quad t>0, (5.2)\\
u(x, 0)=\varphi(x), \quad 0 \leqslant x \leqslant 1, (5.3)
\end{array}\right. ⎩ ⎨ ⎧ ∂ t ∂ u = a ∂ x 2 ∂ 2 u ( a > 0 ) , 0 < t ⩽ T , 0 < x < 1 , ( 5.1 ) u ( 0 , t ) = u ( 1 , t ) = 0 , t > 0 , ( 5.2 ) u ( x , 0 ) = φ ( x ) , 0 ⩽ x ⩽ 1 , ( 5.3 ) 图 5.1 两端固定于冰上的细竿
这就是一维的热传导方程。在研究分子扩散过程(如液体的渗透、半导体材料中杂质的扩散等)时也会遇到类似形式的方程,因而方程(5.1)也叫扩散方程。
定解问题 ( 5.1 ) 、 ( 5.2 ) 、 ( 5.3 ) (5.1)、(5.2)、(5.3) ( 5.1 ) 、 ( 5.2 ) 、 ( 5.3 ) ( 5.1 ) (5.1) ( 5.1 ) ( 5.2 ) (5.2) ( 5.2 )
设 u ( x , t ) = X ( x ) T ( t ) u(x,t)=X(x) T(t) u ( x , t ) = X ( x ) T ( t ) ( 5.1 ) (5.1) ( 5.1 )
X ′ ′ ( x ) X ( x ) = T ′ ( t ) a T ( t ) , (5.4) \frac{X^{\prime \prime}(x)}{X(x)}=\frac{T^{\prime}(t)}{a T(t)},\tag{5.4} X ( x ) X ′′ ( x ) = a T ( t ) T ′ ( t ) , ( 5.4 ) 由于 ( 5.4 ) (5.4) ( 5.4 ) x x x t t t − μ -\mu − μ ( 5.4 ) (5.4) ( 5.4 ) ( 5.2 ) (5.2) ( 5.2 )
{ X ′ ′ + μ X = 0 , X ( 0 ) = X ( 1 ) = 0. (5.5) \left\{\begin{array}{l}
X^{\prime \prime}+\mu X=0, \\
X(0)=X(1)=0.\tag{5.5}
\end{array}\right. { X ′′ + μ X = 0 , X ( 0 ) = X ( 1 ) = 0. ( 5.5 ) T ′ + μ a T = 0. (5.6) T^{\prime}+\mu a T=0.\tag{5.6} T ′ + μ a T = 0. ( 5.6 ) 方程 ( 5.5 ) (5.5) ( 5.5 )
λ 2 + μ = 0 \lambda^2 + \mu = 0 λ 2 + μ = 0
易见,只有当μ > 0 \mu > 0 μ > 0 μ = n 2 π 2 \mu = n^2\pi^2 μ = n 2 π 2 ( 5.5 ) (5.5) ( 5.5 )
X ( x ) = X n ( x ) = sin n π x , (5.7) X(x) = X_n(x) = \sin n\pi x, \tag{5.7} X ( x ) = X n ( x ) = sin nπ x , ( 5.7 ) 此时方程 ( 5.6 ) (5.6) ( 5.6 )
T ( t ) = e − a n 2 π 2 t , (5.8) T(t) = \mathrm{e}^{-an^2\pi^2 t}, \tag{5.8} T ( t ) = e − a n 2 π 2 t , ( 5.8 ) 于是
u ( x , t ) = ∑ n = 1 ∞ α n e − a n 2 π 2 t sin n π x , (5.9) u(x, t) = \sum_{n=1}^{\infty} \alpha_n \mathrm{e}^{-an^2\pi^2 t} \sin n\pi x, \tag{5.9} u ( x , t ) = n = 1 ∑ ∞ α n e − a n 2 π 2 t sin nπ x , ( 5.9 ) 令t = 0 t = 0 t = 0
u ( x , 0 ) = ∑ n = 1 ∞ α n sin n π x = φ ( x ) , u(x, 0) = \sum_{n=1}^{\infty} \alpha_n \sin n\pi x = \varphi(x), u ( x , 0 ) = n = 1 ∑ ∞ α n sin nπ x = φ ( x ) , 因此(5.9)式中的系数 { α n } n = 1 ∞ \{\alpha_n\}_{n=1}^{\infty} { α n } n = 1 ∞ φ ( x ) \varphi(x) φ ( x ) φ ′ ( x ) \varphi^{\prime}(x) φ ′ ( x ) [ 0 , 1 ] [0, 1] [ 0 , 1 ] ( 5.9 ) (5.9) ( 5.9 ) e − a n 2 π 2 t \mathrm{e}^{-an^2\pi^2 t} e − a n 2 π 2 t ( 5.9 ) (5.9) ( 5.9 ) ( 5.1 ) ~ ( 5.3 ) (5.1)~(5.3) ( 5.1 ) ~ ( 5.3 )
若细竿的长度很大,而所需知道的只是在较短时间和较小范围内温度变化的情况,那么边界条件所产生的影响可以忽略,这时可以认为所考察的物体充满整个一维空间,于是可认为方程 ( 5.1 ) (5.1) ( 5.1 ) − ∞ < x < + ∞ -\infty < x < +\infty − ∞ < x < + ∞
u ( x , 0 ) = φ ( x ) , − ∞ < x < ∞ (5.10) u(x, 0) = \varphi(x),\ -\infty < x < \infty \tag{5.10} u ( x , 0 ) = φ ( x ) , − ∞ < x < ∞ ( 5.10 ) 边界条件 ( 5.2 ) (5.2) ( 5.2 )
u ( x , t ) = 1 4 π a t ∫ − ��∞ ∞ e − ( x − ξ ) 2 4 a t φ ( ξ ) d ξ , − ∞ < x < ∞ , t ⩾ 0 (5.11) \begin{align*}
u(x, t) &= \frac{1}{\sqrt{4\pi at}} \int_{-\infty}^{\infty} \mathrm{e}^{-\frac{(x-\xi)^2}{4at}} \varphi(\xi) \mathrm{d}\xi, \\
&-\infty < x < \infty,\ t \geqslant 0
\end{align*}
\tag{5.11} u ( x , t ) = 4 πa t 1 ∫ − ∞ ∞ e − 4 a t ( x − ξ ) 2 φ ( ξ ) d ξ , − ∞ < x < ∞ , t ⩾ 0 ( 5.11 ) 图 5.2 给出了初始(假设为三角形分布)及以后时刻的演化,其特点是波形的棱角消失,逐渐平滑。热传导中的温度变化过程和物质的扩散过程都有这样的性质:不管初始分布如何集中,它总是在瞬间影响到无限——尽管这种影响是随距离的增长而按指数衰减。这是典型的抛物型方程。
图 5.2 扩散方程的演化
2. 波动方程
波��动方程最简单的形式为对流方程:
∂ u ∂ t + a ∂ u ∂ x = 0 , (5.12) \frac{\partial u}{\partial t} + a\frac{\partial u}{\partial x} = 0, \tag{5.12} ∂ t ∂ u + a ∂ x ∂ u = 0 , ( 5.12 ) 设给定的初值条件为
u ( x , 0 ) = φ ( x ) , − ∞ < x < ∞ , (5.13) u(x, 0) = \varphi(x),\ -\infty < x < \infty, \tag{5.13} u ( x , 0 ) = φ ( x ) , − ∞ < x < ∞ , ( 5.13 ) 易见其解为
u ( x , t ) = φ ( x − a t ) , − ∞ < x < ∞ , t ⩾ 0 , (5.14) u(x, t) = \varphi(x - at),\ -\infty < x < \infty,\ t \geqslant 0, \tag{5.14} u ( x , t ) = φ ( x − a t ) , − ∞ < x < ∞ , t ⩾ 0 , ( 5.14 ) 这意味着在O − x t O-xt O − x t x − a t = x - at = x − a t = u u u
如果把 ( 5.13 ) (5.13) ( 5.13 ) t = 0 t = 0 t = 0 ( 5.14 ) (5.14) ( 5.14 ) ∣ a ∣ |a| ∣ a ∣ a > 0 a > 0 a > 0 x x x a < 0 a < 0 a < 0
图 5.3 特征线
x x x
图 5.4 波动方程的演化
对流方程表示的是一个单向传播的波,因而也称作单向波方程。常见的波动方程是
∂ 2 u ∂ t 2 = a 2 ∂ 2 u ∂ x 2 ( a > 0 ) , (5.15) \frac{\partial^2 u}{\partial t^2} = a^2\frac{\partial^2 u}{\partial x^2}\ (a > 0), \tag{5.15} ∂ t 2 ∂ 2 u = a 2 ∂ x 2 ∂ 2 u ( a > 0 ) , ( 5.15 ) 令 v 1 = ∂ u ∂ t , v 2 = a ∂ u ∂ x v_1 = \frac{\partial u}{\partial t},v_2 = a\frac{\partial u}{\partial x} v 1 = ∂ t ∂ u , v 2 = a ∂ x ∂ u
{ ∂ v 1 ∂ t = a ∂ v 2 ∂ x , ∂ v 2 ∂ t = a ∂ v 1 ∂ x . \begin{cases}
\frac{\partial v_1}{\partial t} = a\frac{\partial v_2}{\partial x}, \\
\frac{\partial v_2}{\partial t} = a\frac{\partial v_1}{\partial x}.
\end{cases} { ∂ t ∂ v 1 = a ∂ x ∂ v 2 , ∂ t ∂ v 2 = a ∂ x ∂ v 1 . 再令 w 1 = 1 2 ( v 1 − v 2 ) , w 2 = 1 2 ( v 1 + v 2 ) w_1 = \frac{1}{2}(v_1 - v_2),w_2 = \frac{1}{2}(v_1 + v_2) w 1 = 2 1 ( v 1 − v 2 ) , w 2 = 2 1 ( v 1 + v 2 ) ( 5.15 ) (5.15) ( 5.15 )
{ ∂ w 1 ∂ t + a ∂ w 1 ∂ x = 0 , ∂ w 2 ∂ t − a ∂ w 2 ∂ x = 0. (5.16) \begin{cases}
\frac{\partial w_1}{\partial t} + a\frac{\partial w_1}{\partial x} = 0, \\
\frac{\partial w_2}{\partial t} - a\frac{\partial w_2}{\partial x} = 0.
\end{cases}
\tag{5.16} { ∂ t ∂ w 1 + a ∂ x ∂ w 1 = 0 , ∂ t ∂ w 2 − a ∂ x ∂ w 2 = 0. ( 5.16 ) 这表示方程 ( 5.15 ) (5.15) ( 5.15 )
若方程 ( 5.15 ) (5.15) ( 5.15 )
u ( x , 0 ) = φ ( x ) , ∂ u ( x , 0 ) ∂ t = ψ ( x ) (5.17) u(x, 0) = \varphi(x),\ \frac{\partial u(x, 0)}{\partial t} = \psi(x) \tag{5.17} u ( x , 0 ) = φ ( x ) , ∂ t ∂ u ( x , 0 ) = ψ ( x ) ( 5.17 ) 则其解可由 D'Alembert 公式给出:
u ( x , t ) = φ ( x − a t ) + φ ( x + a t ) 2 + 1 2 a ∫ x − a t x + a t ψ ( ξ ) d ξ (5.18) u(x, t) = \frac{\varphi(x - at) + \varphi(x + at)}{2} + \frac{1}{2a}\int_{x - at}^{x + at} \psi(\xi) d\xi \tag{5.18} u ( x , t ) = 2 φ ( x − a t ) + φ ( x + a t ) + 2 a 1 ∫ x − a t x + a t ψ ( ξ ) d ξ ( 5.18 ) 从 ( 5.18 ) (5.18) ( 5.18 ) u ( x , t ) u(x, t) u ( x , t ) ( x 0 , t 0 ) (x_0, t_0) ( x 0 , t 0 ) x x x [ x 0 − a t 0 , x 0 + a t 0 ] [x_0 - at_0, x_0 + at_0] [ x 0 − a t 0 , x 0 + a t 0 ] ( x 0 , t 0 ) (x_0, t_0) ( x 0 , t 0 ) ( x 0 , t 0 ) (x_0, t_0) ( x 0 , t 0 ) ± 1 a \pm \frac{1}{a} ± a 1 x x x
图 5.5 ( x 0 , t 0 ) (x_0, t_0) ( x 0 , t 0 )
对于波动方程也可以给出一定的边界条件。类似于初边值问题 ( 5.1 ) ~ ( 5.3 ) (5.1)~(5.3) ( 5.1 ) ~ ( 5.3 )
波动方程是典型的双曲型方程,各种不同的双曲型方程,其波的形状、幅度均可有变化,但它总是以有限速度传播,并能保持明确的波阵面——这是这一类方程的共同特点。
3. 对流-扩散方程
在流体的热交换中,对流和传导并存,这时的数学模型成了方程 ( 5.1 ) (5.1) ( 5.1 ) ( 5.12 ) (5.12) ( 5.12 )
∂ u ∂ t + a ∂ u ∂ x − b ∂ 2 u ∂ x 2 = 0 ( b > 0 ) , (5.19) \frac{\partial u}{\partial t} + a\frac{\partial u}{\partial x} - b\frac{\partial^2 u}{\partial x^2} = 0\ (b > 0), \tag{5.19} ∂ t ∂ u + a ∂ x ∂ u − b ∂ x 2 ∂ 2 u = 0 ( b > 0 ) , ( 5.19 ) 它在初始条件 ( 5.10 ) (5.10) ( 5.10 )
u ( x , t ) = 1 4 π b t ∫ − ∞ ∞ e − ( x − ξ − a t ) 2 4 b t φ ( ξ ) d ξ , − ∞ < x < ∞ , t ⩾ 0. (5.20) \begin{align*}
u(x, t) &= \frac{1}{\sqrt{4\pi bt}} \int_{-\infty}^{\infty} \mathrm{e}^{-\frac{(x - \xi - at)^2}{4bt}} \varphi(\xi) d\xi, \\
&-\infty < x < \infty,\ t \geqslant 0.
\end{align*}
\tag{5.20} u ( x , t ) = 4 πb t 1 ∫ − ∞ ∞ e − 4 b t ( x − ξ − a t ) 2 φ ( ξ ) d ξ , − ∞ < x < ∞ , t ⩾ 0. ( 5.20 ) 当 a = 0 a = 0 a = 0 ( 5.11 ) (5.11) ( 5.11 )
图 5.6 表示的是初始为三角分布情况的演化情形。由于方程是由对流和扩散耦合而成的,因此演化兼具两者的特点:一方面平滑,另一方面仿佛以速度 a a a
图 5.6 对流-扩散方程的演化
现实问题所归结出来的偏微分方程,往往要比上面所举出的三种情况复杂得多,如高维(状态除了与 x x x y , z y,z y , z u u u u u u f ( x , t ) f(x, t) f ( x , t ) u u u u u u ( ∂ u ∂ x ) 2 \left(\frac{\partial u}{\partial x}\right)^2 ( ∂ x ∂ u ) 2
y ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 = 0 , y\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0, y ∂ x 2 ∂ 2 u + ∂ y 2 ∂ 2 u = 0 , 在上半平面是椭圆型,在下半平面是双曲型。在空气动力学的跨音速问题中,常遇见这类方程。但对它们进行了适当的限定和处理之后,一般还是可以归结为前述的几种类型之一。下面我们将对典型问题考虑用差分方法来求解。
§2 扩散方程的差分化
§2.1 扩散方程的离散
1. 几种扩散方程的定解问题
先给出几种最简单的扩散方程的定解问题的严格叙述。
(1) 扩散方程初值问题:在区域 D ∞ = { ( x , t ) ∣ − ∞ < x < ∞ , 0 ⩽ t ⩽ T } D_\infty = \{(x, t) | -\infty < x < \infty, 0 \leqslant t \leqslant T\} D ∞ = {( x , t ) ∣ − ∞ < x < ∞ , 0 ⩽ t ⩽ T } u ( x , t ) u(x, t) u ( x , t )
{ ∂ u ∂ t = a ∂ 2 u ∂ x 2 ( a > 0 ) , − ∞ < x < ∞ , 0 < t ⩽ T , u ( x , 0 ) = φ ( x ) , − ∞ < x < ∞ . (5.21) \begin{cases}
\frac{\partial u}{\partial t} = a\frac{\partial^2 u}{\partial x^2}\ (a > 0),\ -\infty < x < \infty,\ 0 < t \leqslant T, \\
u(x, 0) = \varphi(x),\ -\infty < x < \infty.\tag{5.21}
\end{cases}
{ ∂ t ∂ u = a ∂ x 2 ∂ 2 u ( a > 0 ) , − ∞ < x < ∞ , 0 < t ⩽ T , u ( x , 0 ) = φ ( x ) , − ∞ < x < ∞. ( 5.21 ) 这里, φ ( x ) \varphi(x) φ ( x )
(2) 扩散方程初边值问题:这也称为扩散方程的混合问题。下面只给出三种比较典型的,分别称为第一、第二和第三类混合问题,它在给定区域的某段边界上给出的限制条件分别相当于椭圆型方程的齐次的第一、第二和第三类边界条件。
(i) 第一类混合问题:在区域 D I = { ( x , t ) ∣ 0 ⩽ x ⩽ 1 , 0 ⩽ t ⩽ T } D_I = \{(x, t) | 0 \leqslant x \leqslant 1, 0 \leqslant t \leqslant T\} D I = {( x , t ) ∣0 ⩽ x ⩽ 1 , 0 ⩽ t ⩽ T } u ( x , t ) u(x, t) u ( x , t )
{ ∂ u ∂ t = a ∂ 2 u ∂ x 2 ( a > 0 ) , 0 < x < 1 , 0 < t ⩽ T , u ( x , 0 ) = φ ( x ) , 0 < x < 1 , u ( 0 , t ) = u ( 1 , t ) = 0 , 0 ⩽ t ⩽ T . (5.22) \begin{cases}
\frac{\partial u}{\partial t} = a\frac{\partial^2 u}{\partial x^2}\ (a > 0),\ 0 < x < 1,\ 0 < t \leqslant T, \\
u(x, 0) = \varphi(x),\ 0 < x < 1, \\
u(0, t) = u(1, t) = 0,\ 0 \leqslant t \leqslant T. \tag{5.22}
\end{cases}
⎩ ⎨ ⎧ ∂ t ∂ u = a ∂ x 2 ∂ 2 u ( a > 0 ) , 0 < x < 1 , 0 < t ⩽ T , u ( x , 0 ) = φ ( x ) , 0 < x < 1 , u ( 0 , t ) = u ( 1 , t ) = 0 , 0 ⩽ t ⩽ T . ( 5.22 ) (ii) 第二类混合问题:在区域 D I D_I D I u ( x , t ) u(x, t) u ( x , t )
{ ∂ u ∂ t = a ∂ 2 u ∂ x 2 ( a > 0 ) , 0 < x < 1 , 0 < t ⩽ T , u ( x , 0 ) = φ ( x ) , 0 < x < 1 , u ( 0 , t ) = ∂ u ( 1 , t ) ∂ x = 0 , 0 ⩽ t ⩽ T . (5.23) \begin{cases}
\frac{\partial u}{\partial t} = a\frac{\partial^2 u}{\partial x^2}\ (a > 0),\ 0 < x < 1,\ 0 < t \leqslant T, \\
u(x, 0) = \varphi(x),\ 0 < x < 1, \\
u(0, t) = \frac{\partial u(1, t)}{\partial x} = 0,\ 0 \leqslant t \leqslant T. \tag{5.23}
\end{cases} ⎩ ⎨ ⎧ ∂ t ∂ u = a ∂ x 2 ∂ 2 u ( a > 0 ) , 0 < x < 1 , 0 < t ⩽ T , u ( x , 0 ) = φ ( x ) , 0 < x < 1 , u ( 0 , t ) = ∂ x ∂ u ( 1 , t ) = 0 , 0 ⩽ t ⩽ T . ( 5.23 ) (iii) 第三类混合问题:在区域D I D_I D I u ( x , t ) u(x, t) u ( x , t )
{ ∂ u ∂ t = a ∂ 2 u ∂ x 2 ( a > 0 ) , 0 < x < 1 , 0 < t ⩽ T , u ( x , 0 ) = φ ( x ) , 0 < x < 1 , u ( 0 , t ) = ∂ u ( 1 , t ) ∂ x + α u ( 1 , t ) = 0 ( α > 0 ) , 0 ⩽ t ⩽ T . (5.24) \begin{cases}
\frac{\partial u}{\partial t} = a\frac{\partial^2 u}{\partial x^2}\ (a > 0),\ 0 < x < 1,\ 0 < t \leqslant T, \\
u(x, 0) = \varphi(x),\ 0 < x < 1, \\
u(0, t) = \frac{\partial u(1, t)}{\partial x} + \alpha u(1, t) = 0\ (\alpha > 0),\ 0 \leqslant t \leqslant T.\tag{5.24}
\end{cases} ⎩ ⎨ ⎧ ∂ t ∂ u = a ∂ x 2 ∂ 2 u ( a > 0 ) , 0 < x < 1 , 0 < t ⩽ T , u ( x , 0 ) = φ ( x ) , 0 < x < 1 , u ( 0 , t ) = ∂ x ∂ u ( 1 , t ) + αu ( 1 , t ) = 0 ( α > 0 ) , 0 ⩽ t ⩽ T . ( 5.24 ) 2. 差分方法求解的过程
用差分方法求解上述问题的过程与第三章中解椭圆方程的过程是完全相同的,可分为区域离散,方程离散和截断误差估计,初边值处理,差分解的存在唯一性、稳定性、收敛性分析,差分方程求解等步骤。下面先以混合问题为例来叙述上述过程。
(1) 区域的离散:设N N N h = 1 N h = \frac{1}{N} h = N 1 τ \tau τ τ < T \tau < T τ < T x x x t t t
x = x i = i h , i = 0 , 1 , 2 , ⋯ , N , t = t j = j τ , j = 0 , 1 , 2 , ⋯ , m = [ T τ ] x = x_i = ih,\ i = 0, 1, 2, \cdots, N,\\
t = t_j = j\tau,\ j = 0, 1, 2, \cdots, m = \left[\frac{T}{\tau}\right] x = x i = ih , i = 0 , 1 , 2 , ⋯ , N , t = t j = j τ , j = 0 , 1 , 2 , ⋯ , m = [ τ T ] ( [ x ] [x] [ x ] x x x D I D_I D I x = x i x = x_i x = x i t = t j t = t_j t = t j ( x i , t j ) (x_i, t_j) ( x i , t j )
在 x = 0 x = 0 x = 0 x = 1 x = 1 x = 1 t = 0 t = 0 t = 0 u i j u_i^j u i j ( x i , t j ) (x_i, t_j) ( x i , t j ) u ( x i , t j ) u(x_i, t_j) u ( x i , t j )
图 5.7 区域的剖分
(2) 方程的离散
这里采用直接差分法,即用差商代替微商。现考虑在 ( x i , t j ) (x_i, t_j) ( x i , t j ) u ( x i , t j ) u(x_i, t_j) u ( x i , t j ) t t t 向后差商 来代替 ∂ u ( x i , t j ) ∂ t \frac{\partial u(x_i, t_j)}{\partial t} ∂ t ∂ u ( x i , t j ) j j j t = t j t = t_j t = t j j + 1 j + 1 j + 1 ∂ 2 u ( x i , t j ) ∂ x 2 \frac{\partial^2 u(x_i, t_j)}{\partial x^2} ∂ x 2 ∂ 2 u ( x i , t j )
u i j + 1 − u i j τ − [ a θ u i + 1 j + 1 − 2 u i j + 1 + u i − 1 j + 1 h 2 + a ( 1 − θ ) u i + 1 j − 2 u i j + u i − 1 j h 2 ] = 0 , 0 ⩽ θ ⩽ 1. \begin{align*}
&\frac{u_i^{j+1} - u_i^j}{\tau} - \left[a\theta \frac{u_{i+1}^{j+1} - 2u_i^{j+1} + u_{i-1}^{j+1}}{h^2} + a(1 - \theta) \frac{u_{i+1}^j - 2u_i^j + u_{i-1}^j}{h^2}\right] = 0, \\
&0 \leqslant \theta \leqslant 1. \tag{5.25}
\end{align*}
τ u i j + 1 − u i j − [ a θ h 2 u i + 1 j + 1 − 2 u i j + 1 + u i − 1 j + 1 + a ( 1 − θ ) h 2 u i + 1 j − 2 u i j + u i − 1 j ] = 0 , 0 ⩽ θ ⩽ 1. ( 5.25 ) 这样的格式称为两层加权平均格式 。
若将微分方程的真解 u ( x , t ) u(x, t) u ( x , t ) ( 5.25 ) (5.25) ( 5.25 ) ( 5.25 ) (5.25) ( 5.25 ) 截断误差 。
将方程 ( 5.25 ) (5.25) ( 5.25 ) u ( x , t ) u(x, t) u ( x , t ) ( x i , t j ) (x_i, t_j) ( x i , t j ) u ( x , t ) u(x, t) u ( x , t )
u ( x i , t j + 1 ) − u ( x i , t j ) τ = ∂ u ∂ t ( x i , t j ) + τ 2 ∂ 2 u ∂ t 2 ( x i , t j ) + O ( τ 2 ) = ∂ u ∂ t ( x i , t j ) + a 2 τ 2 ∂ 4 u ∂ x 4 ( x i , t j ) + O ( τ 2 ) , \begin{align*}
&\frac{u(x_i, t_{j+1}) - u(x_i, t_j)}{\tau} \\
&= \frac{\partial u}{\partial t}(x_i, t_j) + \frac{\tau}{2} \frac{\partial^2 u}{\partial t^2}(x_i, t_j) + O(\tau^2) \\
&= \frac{\partial u}{\partial t}(x_i, t_j) + \frac{a^2 \tau}{2} \frac{\partial^4 u}{\partial x^4}(x_i, t_j) + O(\tau^2),\tag{5.26}
\end{align*} τ u ( x i , t j + 1 ) − u ( x i , t j ) = ∂ t ∂ u ( x i , t j ) + 2 τ ∂ t 2 ∂ 2 u ( x i , t j ) + O ( τ 2 ) = ∂ t ∂ u ( x i , t j ) + 2 a 2 τ ∂ x 4 ∂ 4 u ( x i , t j ) + O ( τ 2 ) , ( 5.26 ) u ( x i + 1 , t j + 1 ) − 2 u ( x i , t j + 1 ) + u ( x i − 1 , t j + 1 ) h 2 = ∂ 2 u ∂ x 2 ( x i , t j + 1 ) + h 2 12 ∂ 4 u ∂ x 4 ( x i , t j + 1 ) + O ( h 4 ) = [ ∂ 2 u ∂ x 2 ( x i , t j ) + τ ∂ ∂ t ∂ 2 u ∂ x 2 ( x i , t j ) + O ( τ 2 ) ] + h 2 12 [ ∂ 4 u ∂ x 4 ( x i , t j ) + τ ∂ ∂ t ∂ 4 u ∂ x 4 ( x i , t j ) + O ( τ 2 ) ] + O ( h 4 ) = ∂ 2 u ∂ x 2 ( x i , t j ) + h 2 + a τ 12 ∂ 4 u ∂ x 4 ( x i , t j ) + O ( τ 2 ) + O ( τ h 2 ) + O ( h 4 ) , \begin{align*}
&\frac{u(x_{i+1}, t_{j+1}) - 2u(x_i, t_{j+1}) + u(x_{i-1}, t_{j+1})}{h^2} \\
&= \frac{\partial^2 u}{\partial x^2}(x_i, t_{j+1}) + \frac{h^2}{12} \frac{\partial^4 u}{\partial x^4}(x_i, t_{j+1}) + O(h^4) \\
&= \left[\frac{\partial^2 u}{\partial x^2}(x_i, t_j) + \tau \frac{\partial}{\partial t} \frac{\partial^2 u}{\partial x^2}(x_i, t_j) + O(\tau^2)\right] \\\tag{5.27}
&\quad + \frac{h^2}{12}\left[\frac{\partial^4 u}{\partial x^4}(x_i, t_j) + \tau \frac{\partial}{\partial t} \frac{\partial^4 u}{\partial x^4}(x_i, t_j) + O(\tau^2)\right] + O(h^4) \\
&= \frac{\partial^2 u}{\partial x^2}(x_i, t_j) + \frac{h^2 + a\tau}{12} \frac{\partial^4 u}{\partial x^4}(x_i, t_j) + O(\tau^2) + O(\tau h^2) + O(h^4),
\end{align*} h 2 u ( x i + 1 , t j + 1 ) − 2 u ( x i , t j + 1 ) + u ( x i − 1 , t j + 1 ) = ∂ x 2 ∂ 2 u ( x i , t j + 1 ) + 12 h 2 ∂ x 4 ∂ 4 u ( x i , t j + 1 ) + O ( h 4 ) = [ ∂ x 2 ∂ 2 u ( x i , t j ) + τ ∂ t ∂ ∂ x 2 ∂ 2 u ( x i , t j ) + O ( τ 2 ) ] + 12 h 2 [ ∂ x 4 ∂ 4 u ( x i , t j ) + τ ∂ t ∂ ∂ x 4 ∂ 4 u ( x i , t j ) + O ( τ 2 ) ] + O ( h 4 ) = ∂ x 2 ∂ 2 u ( x i , t j ) + 12 h 2 + a τ ∂ x 4 ∂ 4 u ( x i , t j ) + O ( τ 2 ) + O ( τ h 2 ) + O ( h 4 ) , ( 5.27 ) u ( x i + 1 , t j ) − 2 u ( x i , t j ) + u ( x i − 1 , t j ) h 2 = ∂ 2 u ∂ x 2 ( x i , t j ) + h 2 12 ∂ 4 u ∂ x 4 ( x i , t j ) + O ( h 4 ) . (5.28) \begin{align*}
&\frac{u(x_{i+1}, t_j) - 2u(x_i, t_j) + u(x_{i-1}, t_j)}{h^2} \\
&= \frac{\partial^2 u}{\partial x^2}(x_i, t_j) + \frac{h^2}{12} \frac{\partial^4 u}{\partial x^4}(x_i, t_j) + O(h^4).
\end{align*}
\tag{5.28} h 2 u ( x i + 1 , t j ) − 2 u ( x i , t j ) + u ( x i − 1 , t j ) = ∂ x 2 ∂ 2 u ( x i , t j ) + 12 h 2 ∂ x 4 ∂ 4 u ( x i , t j ) + O ( h 4 ) . ( 5.28 ) 将 ( 5.27 ) (5.27) ( 5.27 ) ( − a θ ) (-a\theta) ( − a θ ) ( 5.28 ) (5.28) ( 5.28 ) ( − a ( 1 − θ ) ) (-a(1 - \theta)) ( − a ( 1 − θ )) ( 5.26 ) (5.26) ( 5.26 ) R i j ( θ ) R_i^j(\theta) R i j ( θ ) 局部截断误差 (以下简称为截断误差),便有
R i j ( θ ) = a [ a τ ( 1 2 − θ ) − h 2 12 ] ∂ 4 u ∂ x 4 ( x i , t j ) + O ( τ 2 ) + O ( τ h 2 ) + O ( h 4 ) . \begin{align*}
R_i^j(\theta) &= a\left[a\tau \left(\frac{1}{2} - \theta\right) - \frac{h^2}{12}\right] \frac{\partial^4 u}{\partial x^4}(x_i, t_j) \\
&\quad + O(\tau^2) + O(\tau h^2) + O(h^4).\tag{5.29}
\end{align*} R i j ( θ ) = a [ a τ ( 2 1 − θ ) − 12 h 2 ] ∂ x 4 ∂ 4 u ( x i , t j ) + O ( τ 2 ) + O ( τ h 2 ) + O ( h 4 ) . ( 5.29 ) 微分方程还可用其他方式离散,如用 u ( x i , t j ) u(x_i, t_j) u ( x i , t j ) t t t ∂ 2 u ∂ x 2 \frac{\partial^2 u}{\partial x^2} ∂ x 2 ∂ 2 u j j j x x x ∂ 2 u ∂ x 2 \frac{\partial^2 u}{\partial x^2} ∂ x 2 ∂ 2 u
u i j + 1 − u i j − 1 2 τ − a u i + 1 j − 2 u i j + u i − 1 j h 2 = 0. (5.30) \frac{u_i^{j+1} - u_i^{j-1}}{2\tau} - a\frac{u_{i+1}^j - 2u_i^j + u_{i-1}^j}{h^2} = 0. \tag{5.30} 2 τ u i j + 1 − u i j − 1 − a h 2 u i + 1 j − 2 u i j + u i − 1 j = 0. ( 5.30 ) 这是一个三层格式,易知它的截断误差为
R i j = τ 2 6 ∂ 3 u ∂ t 3 ( x i , t j ) − a h 2 12 ∂ 4 u ∂ x 4 ( x i , t j ) + O ( τ 2 ) + O ( h 4 ) . R_i^j = \frac{\tau^2}{6} \frac{\partial^3 u}{\partial t^3}(x_i, t_j) - \frac{ah^2}{12} \frac{\partial^4 u}{\partial x^4}(x_i, t_j) + O(\tau^2) + O(h^4). R i j = 6 τ 2 ∂ t 3 ∂ 3 u ( x i , t j ) − 12 a h 2 ∂ x 4 ∂ 4 u ( x i , t j ) + O ( τ 2 ) + O ( h 4 ) . (3) 初始条件的离散:以下假定 φ ( x ) \varphi(x) φ ( x ) { x i } i = 0 N − 1 \{x_i\}_{i=0}^{N-1} { x i } i = 0 N − 1 u i 0 = φ ( x i ) ≜ φ i ( i = 1 , 2 , ⋯ , N − 1 ) u_i^0 = \varphi(x_i) \triangleq \varphi_i(i = 1, 2, \cdots, N - 1) u i 0 = φ ( x i ) ≜ φ i ( i = 1 , 2 , ⋯ , N − 1 ) φ ( x ) \varphi(x) φ ( x )
(4) 边界条件的离散:
(i) 第一类混合问题边界条件的离散:只要取 u 0 j = u N j = 0 ( j = 0 , 1 , 2 , ⋯ , m ) u_0^j = u_N^j = 0\ (j = 0, 1, 2, \cdots, m) u 0 j = u N j = 0 ( j = 0 , 1 , 2 , ⋯ , m )
(ii) 第二类混合问题边界条件的离散:在左边界 x = 0 x = 0 x = 0 x = 1 x = 1 x = 1
u N j − u N − 1 j = 0 ( j = 0 , 1 , 2 , ⋯ , m ) . (5.32) u_N^j - u_{N-1}^j = 0\ (j = 0, 1, 2, \cdots, m). \tag{5.32} u N j − u N − 1 j = 0 ( j = 0 , 1 , 2 , ⋯ , m ) . ( 5.32 )
(iii) 第三类混合问题边界条件的离散:在左边界 x = 0 x = 0 x = 0 x = 1 x = 1 x = 1
u N j − u N − 1 j h + α u N j = 0. \frac{u_N^j - u_{N-1}^j}{h} + \alpha u_N^j = 0. h u N j − u N − 1 j + α u N j = 0. 或写成
( 1 + α h ) u N j − u N − 1 j = 0 , ( j = 0 , 1 , 2 , ⋯ , m ) . (5.33) (1 + \alpha h)u_N^j - u_{N-1}^j = 0,\ (j = 0, 1, 2, \cdots, m). \tag{5.33} ( 1 + α h ) u N j − u N − 1 j = 0 , ( j = 0 , 1 , 2 , ⋯ , m ) . ( 5.33 ) §2.2 计算格式示例
以下讨论一般都以第一类混合问题为对象,其方法和结论不难平行地推广到其他类型的混合问题中去。
这里先列举出一些差分格式,为简单起见,除了第一个格式外,将不再列出边界点的处理。
记 r = a τ h 2 r = \frac{a\tau}{h^2} r = h 2 a τ τ \tau τ h h h r r r
利用 r r r ( 5.25 ) (5.25) ( 5.25 )
u i j + 1 = r ( 1 − θ ) u i + 1 j + ( 1 − 2 r ( 1 − θ ) ) u i j + r ( 1 − θ ) u i − 1 j + r θ u i + 1 j + 1 + ( 1 − 2 r θ ) u i j + 1 + r θ u i − 1 j + 1 . (5.34) u_i^{j+1} = r(1 - \theta)u_{i+1}^j + (1 - 2r(1 - \theta))u_i^j + r(1 - \theta)u_{i-1}^j + r\theta u_{i+1}^{j+1} + (1 - 2r\theta)u_i^{j+1} + r\theta u_{i-1}^{j+1}. \tag{5.34} u i j + 1 = r ( 1 − θ ) u i + 1 j + ( 1 − 2 r ( 1 − θ )) u i j + r ( 1 − θ ) u i − 1 j + r θ u i + 1 j + 1 + ( 1 − 2 r θ ) u i j + 1 + r θ u i − 1 j + 1 . ( 5.34 ) 1. 古典显格式
在方程 ( 5.34 ) (5.34) ( 5.34 ) θ = 0 \theta = 0 θ = 0
{ u i j + 1 = r u i + 1 j + ( 1 − 2 r ) u i j + r u i − 1 j , i = 1 , 2 , ⋯ , N − 1 , j = 0 , 1 , 2 , ⋯ , m − 1 , u i 0 = φ ( x i ) = φ i , i = 1 , 2 , ⋯ , N − 1 , u 0 j = u N j = 0 , j = 0 , 1 , 2 , ⋯ , m (5.35) \begin{cases}
u_i^{j+1} = ru_{i+1}^j + (1 - 2r)u_i^j + ru_{i-1}^j,\quad i = 1, 2, \cdots, N - 1,\ j = 0, 1, 2, \cdots, m - 1,\\
u_i^0 = \varphi(x_i) = \varphi_i,\ i = 1, 2, \cdots, N - 1,
u_0^j = u_N^j = 0,\ j = 0, 1, 2, \cdots, m \tag{5.35}
\end{cases} { u i j + 1 = r u i + 1 j + ( 1 − 2 r ) u i j + r u i − 1 j , i = 1 , 2 , ⋯ , N − 1 , j = 0 , 1 , 2 , ⋯ , m − 1 , u i 0 = φ ( x i ) = φ i , i = 1 , 2 , ⋯ , N − 1 , u 0 j = u N j = 0 , j = 0 , 1 , 2 , ⋯ , m ( 5.35 ) 用记号 ⊗ \otimes ⊗ × \times × x x x t t t
图 5.8 古典显格式
由 ( 5.29 ) (5.29) ( 5.29 ) R i j ( θ ) = O ( τ + h 2 ) R_i^j(\theta) = O(\tau + h^2) R i j ( θ ) = O ( τ + h 2 )
格式 ( 5.35 ) (5.35) ( 5.35 )
先在 ( 5.35 ) (5.35) ( 5.35 ) j = 0 j = 0 j = 0 u i 0 = φ i u_i^0 = \varphi_i u i 0 = φ i u i − 1 0 , u i 0 , u i + 1 0 u_{i-1}^0,u_i^0,u^0_{i+1} u i − 1 0 , u i 0 , u i + 1 0 u i 1 ( i = 1 , 2 , ⋯ , N − 1 ) u_i^1(i = 1, 2, \cdots, N - 1) u i 1 ( i = 1 , 2 , ⋯ , N − 1 ) u 0 1 , u N 1 u_0^1, u_N^1 u 0 1 , u N 1 u i − 1 1 , u i 1 , u i + 1 1 u_{i-1}^1, u_i^1, u_{i+1}^1 u i − 1 1 , u i 1 , u i + 1 1 u i 2 ( i = 1 , 2 , ⋯ , N − 1 ) u_i^2(i = 1, 2, \cdots, N - 1) u i 2 ( i = 1 , 2 , ⋯ , N − 1 ) m m m
在计算第 j + 1 j + 1 j + 1 j j j
2. 古典隐格式
在方程 ( 5.34 ) (5.34) ( 5.34 ) θ = 1 \theta = 1 θ = 1
{ − r u i + 1 j + 1 + ( 1 + 2 r ) u i j + 1 − r u i − 1 j + 1 = u i j , i = 1 , 2 , ⋯ , N − 1 , j = 0 , 1 , ⋯ , m − 1. (5.36) \begin{cases}
-ru_{i+1}^{j+1} + (1 + 2r)u_i^{j+1} - ru_{i-1}^{j+1} = u_i^j, \\
i = 1, 2, \cdots, N - 1, \\
j = 0, 1, \cdots, m - 1. \tag{5.36}
\end{cases} ⎩ ⎨ ⎧ − r u i + 1 j + 1 + ( 1 + 2 r ) u i j + 1 − r u i − 1 j + 1 = u i j , i = 1 , 2 , ⋯ , N − 1 , j = 0 , 1 , ⋯ , m − 1. ( 5.36 ) 图 5.9 古典隐格式
它所用的结点可以图表示出来(图 5.9),其截断误差的阶与古典显格式是相同的:
R i j ( 1 ) = O ( τ + h 2 ) . R_i^j(1) = O(\tau + h^2). R i j ( 1 ) = O ( τ + h 2 ) . 格式 ( 5.36 ) (5.36) ( 5.36 )
首先在 ( 5.36 ) (5.36) ( 5.36 ) j = 0 j = 0 j = 0 u 1 1 , u 2 1 , ⋯ , u N − 1 1 u_1^1, u_2^1, \cdots, u_{N-1}^1 u 1 1 , u 2 1 , ⋯ , u N − 1 1
[ 1 + 2 r − r − r 1 + 2 r − r − r ⋱ ⋱ − r 1 + 2 r ] [ u 1 1 u 2 1 ⋮ u N − 1 1 ] = [ u 1 0 u 2 0 ⋮ u N − 1 0 ] ( 即 [ φ 1 φ 2 ⋮ φ N − 1 ] ) (5.37) \begin{bmatrix}
1 + 2r & -r \\
-r & 1 + 2r & -r \\
& -r & \ddots & \ddots \\
& & -r & 1 + 2r
\end{bmatrix}
\begin{bmatrix}
u_1^1 \\
u_2^1 \\
\vdots \\
u_{N-1}^1
\end{bmatrix}
=
\begin{bmatrix}
u_1^0 \\
u_2^0 \\
\vdots \\
u_{N-1}^0
\end{bmatrix}
\quad
(即\quad
\begin{bmatrix}
\varphi_1 \\
\varphi_2 \\
\vdots \\
\varphi_{N-1}
\end{bmatrix}
)
\tag{5.37} 1 + 2 r − r − r 1 + 2 r − r − r ⋱ − r ⋱ 1 + 2 r u 1 1 u 2 1 ⋮ u N − 1 1 = u 1 0 u 2 0 ⋮ u N − 1 0 ( 即 φ 1 φ 2 ⋮ φ N − 1 ) ( 5.37 ) 因而需要解一个系数矩阵为对称正定的三对角方程来求出第一层上的近似值。
接着,令 j = 1 j = 1 j = 1 ( 5.37 ) (5.37) ( 5.37 ) m m m
在现在讨论的情况中,所有层数的方程组的系数矩阵都是相同的。所以,可以在一开始先将它作一个 Cholesky 分解后存贮起来,以后每一层要用时就可减少工作量。
像这样在求第 j + 1 j + 1 j + 1
3. Crank-Nicholson 格式
在方程(5.34)中令θ = 1 2 \theta = \frac{1}{2} θ = 2 1
{ − r 2 u i + 1 j + 1 + ( 1 + r ) u i j + 1 − r 2 u i − 1 j + 1 = r 2 u i + 1 j + ( 1 − r ) u i j + r 2 u i − 1 j , i = 1 , 2 , ⋯ , N − 1 , j = 0 , 1 , ⋯ , m − 1. (5.38) \begin{cases}
-\frac{r}{2}u_{i+1}^{j+1} + (1 + r)u_i^{j+1} - \frac{r}{2}u_{i-1}^{j+1} \\
\quad = \frac{r}{2}u_{i+1}^j + (1 - r)u_i^j + \frac{r}{2}u_{i-1}^j, \\
i = 1, 2, \cdots, N - 1, \\
j = 0, 1, \cdots, m - 1. \tag{5.38}
\end{cases}
⎩ ⎨ ⎧ − 2 r u i + 1 j + 1 + ( 1 + r ) u i j + 1 − 2 r u i − 1 j + 1 = 2 r u i + 1 j + ( 1 − r ) u i j + 2 r u i − 1 j , i = 1 , 2 , ⋯ , N − 1 , j = 0 , 1 , ⋯ , m − 1. ( 5.38 ) 这个格式所用的结点如图 5.10 所示。
图 5.10 Crank-Nicholson 格式
各层右边的数字“1 2 \frac{1}{2} 2 1 ∂ 2 u ∂ x 2 \frac{\partial^2 u}{\partial x^2} ∂ x 2 ∂ 2 u x x x
在(5.29)中令θ = 1 2 \theta = \frac{1}{2} θ = 2 1 R i j ( 1 2 ) = O ( τ 2 + h 2 ) R_i^j\left(\frac{1}{2}\right) = O(\tau^2 + h^2) R i j ( 2 1 ) = O ( τ 2 + h 2 )
六点对称格式 显然是个隐格式,在由第j j j j + 1 j + 1 j + 1
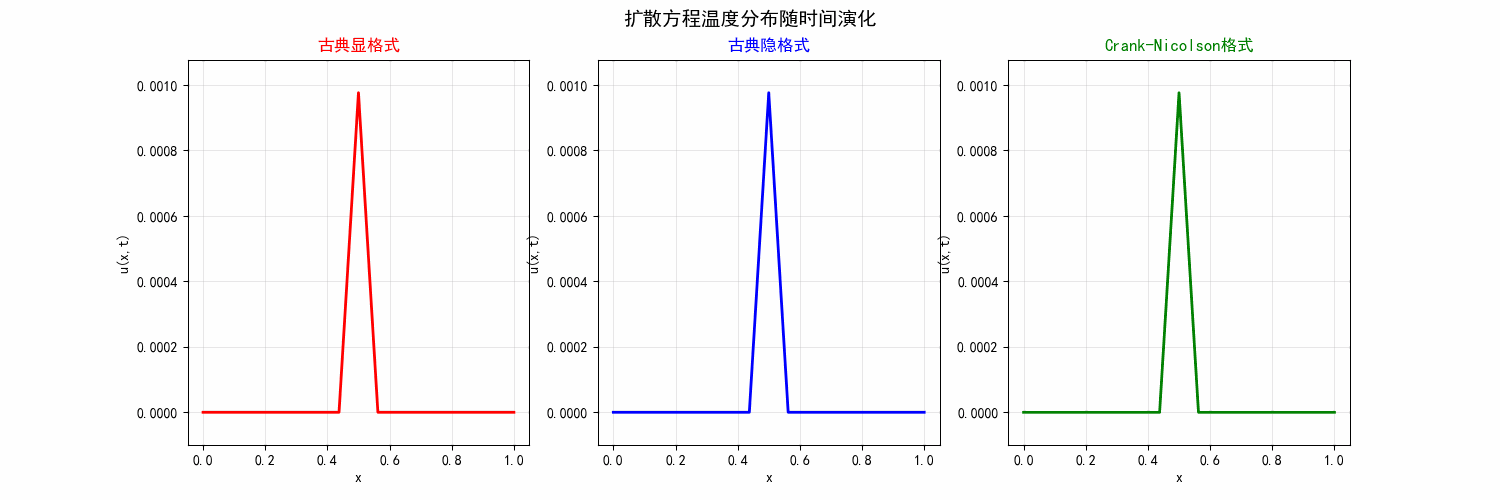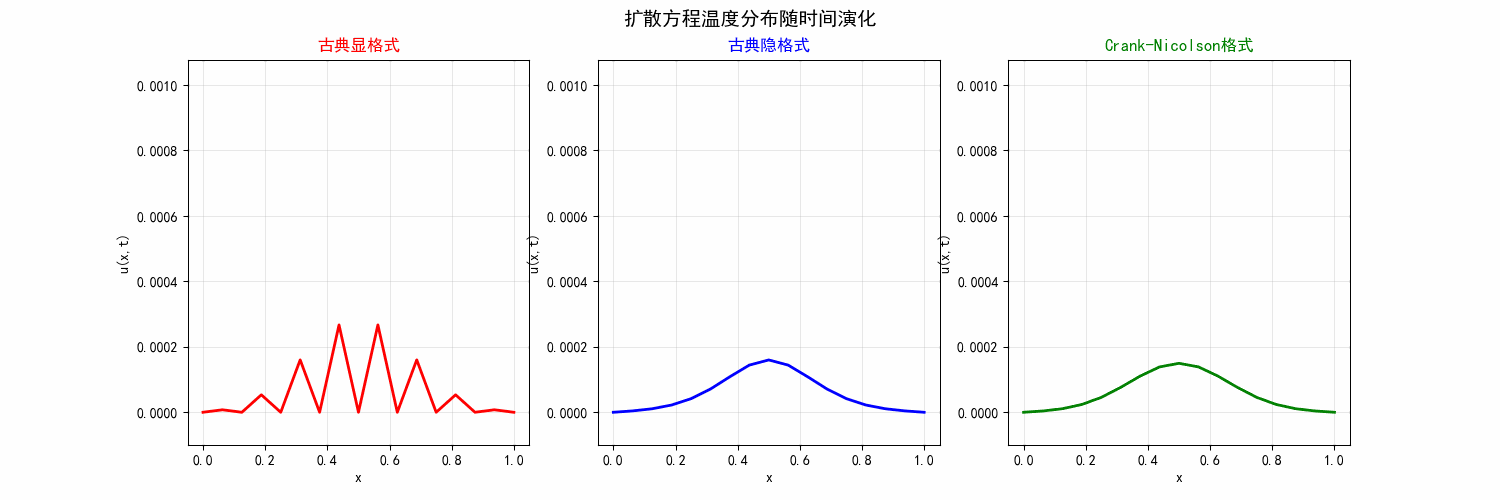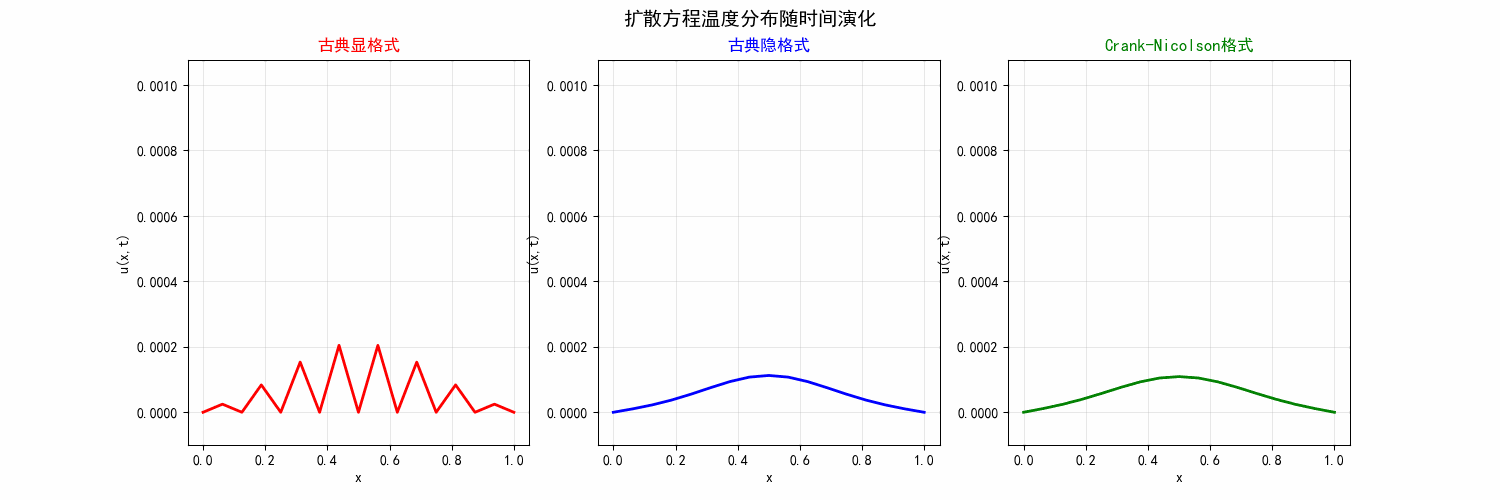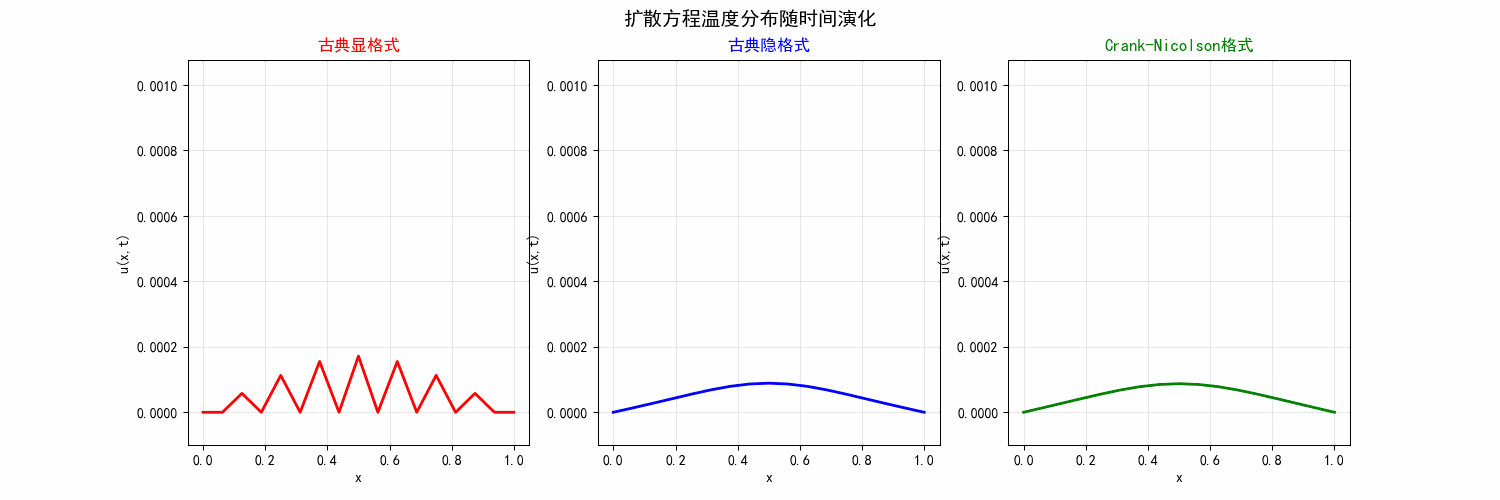
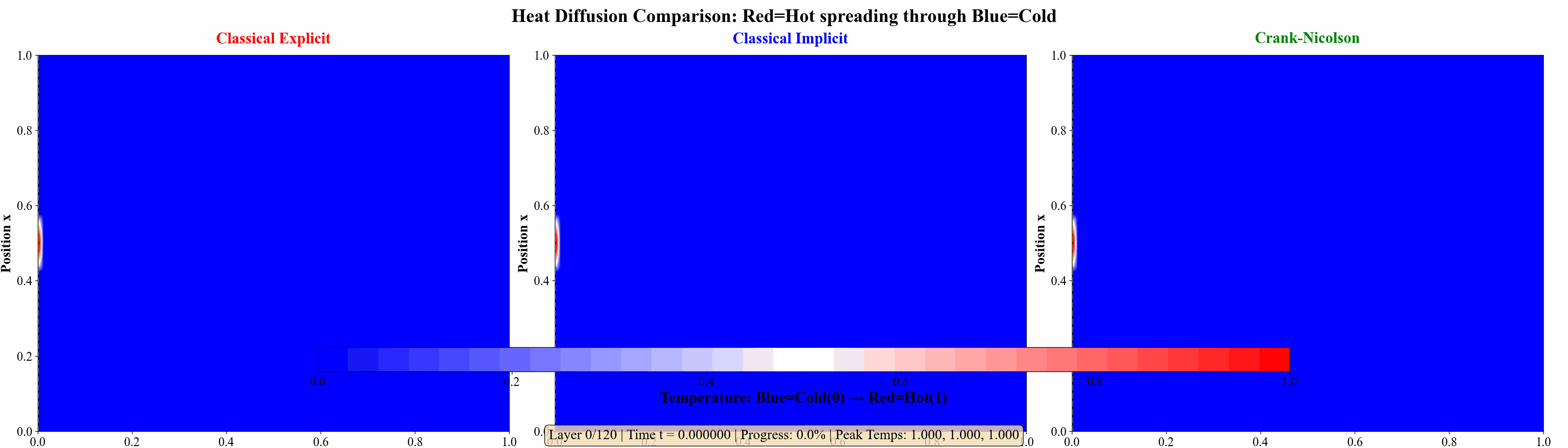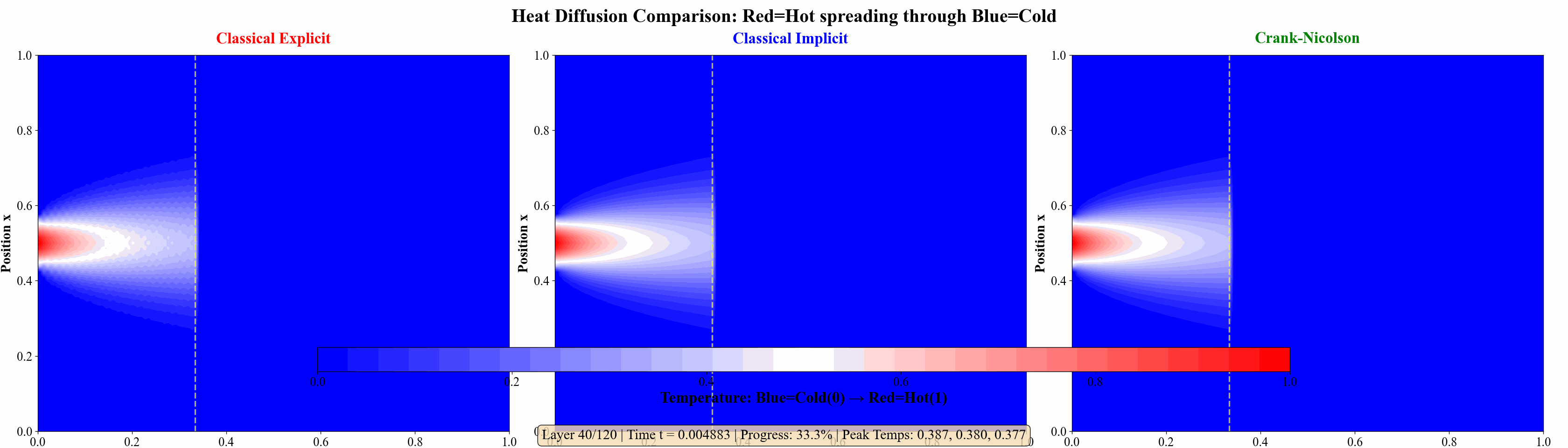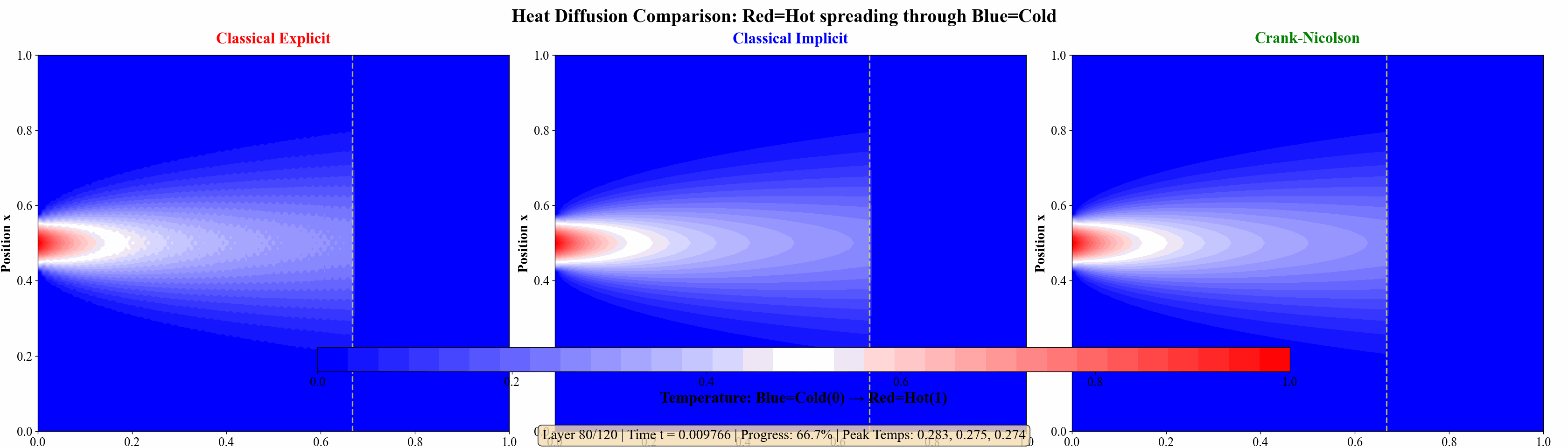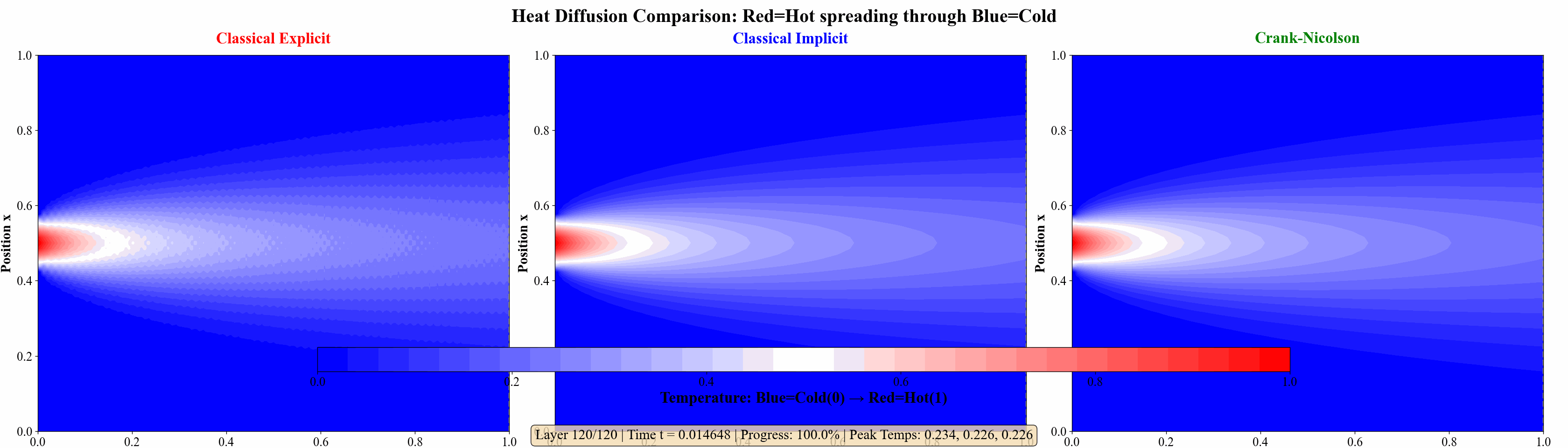
Example 1
对定解问题:
{ ∂ u ∂ t = ∂ 2 u ∂ x 2 , x ∈ ( 0 , 1 ) , t ∈ ( 0 , T ] , u ( 0 , t ) = u ( 1 , t ) = 0 , t ∈ ( 0 , T ] , u ( x , 0 ) = 0 , x ∈ ( 0 , 1 ) . \begin{cases}
\frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x^2}, & x \in (0,1), t \in (0,T], \\
u(0,t) = u(1,t) = 0, & t \in (0,T], \\
u(x,0) = 0, & x \in (0,1).
\end{cases} ⎩ ⎨ ⎧ ∂ t ∂ u = ∂ x 2 ∂ 2 u , u ( 0 , t ) = u ( 1 , t ) = 0 , u ( x , 0 ) = 0 , x ∈ ( 0 , 1 ) , t ∈ ( 0 , T ] , t ∈ ( 0 , T ] , x ∈ ( 0 , 1 ) . 若在 u ( 1 2 , 0 ) u\left(\frac{1}{2}, 0\right) u ( 2 1 , 0 ) 1 2 10 \frac{1}{2^{10}} 2 10 1 h = 1 16 h=\frac{1}{16} h = 16 1 r = 1 2 r=\frac{1}{2} r = 2 1
打印出第 8 层上各结点处的计算值;
预测继续算下去计算值的变化趋势;
分析上述趋势产生的原因。
我们实现了相关代码放在了 Github 上,可见https://github.com/FEMATHS/Example/tree/main/ch3/section2/example1 ,效果如下:
图 1:显式格式计算第八层
图 2:显式格式计算第八层的误差
图 3:隐式格式计算第八层
图 4:隐式格式计算第八层的误差
图 5:Crank–Nicolson格式计算第八层
图 6:Crank–Nicolson格式计算第八层的误差
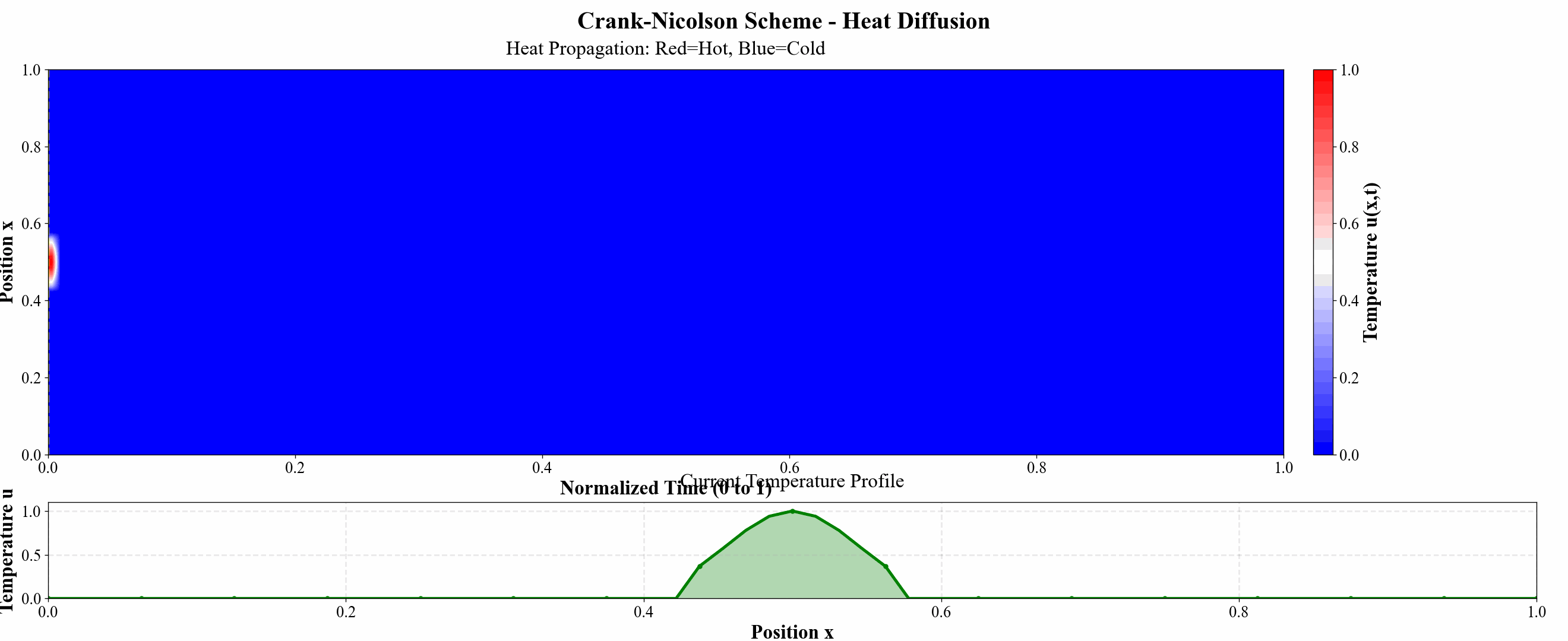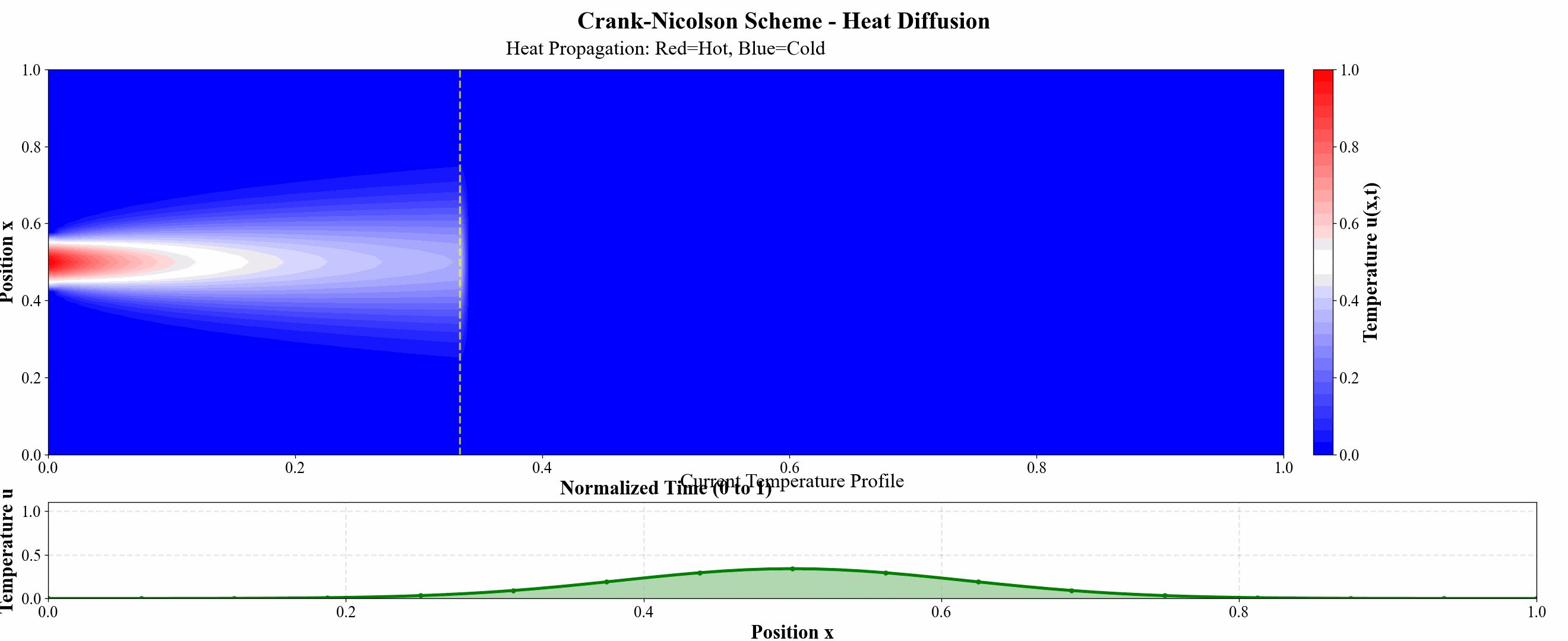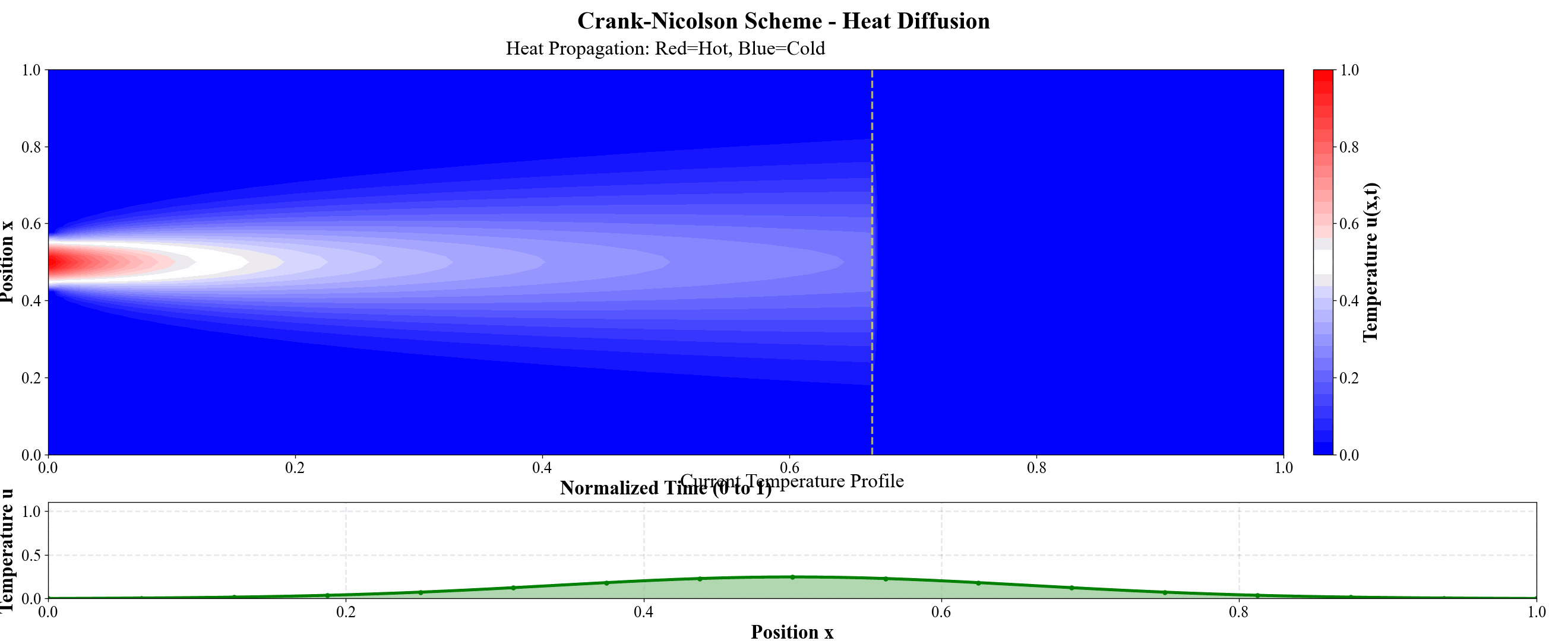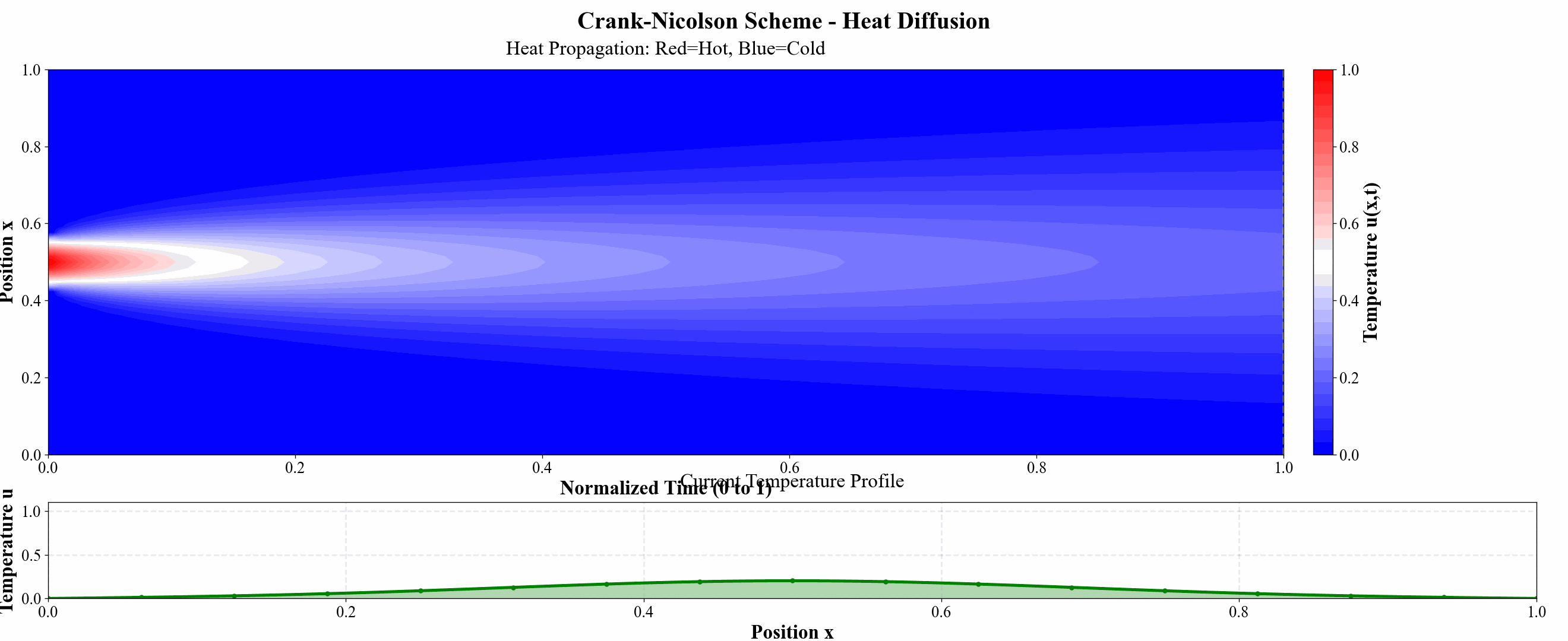
为进一步说明例子,我还做了几张热力图说明问题:
图 7 三种格式(显式格式、隐式格式、Crank–Nicolson 格式) 的比较
图 8 三种格式(显式格式、隐式格式、Crank–Nicolson 格式) 的热力图比较
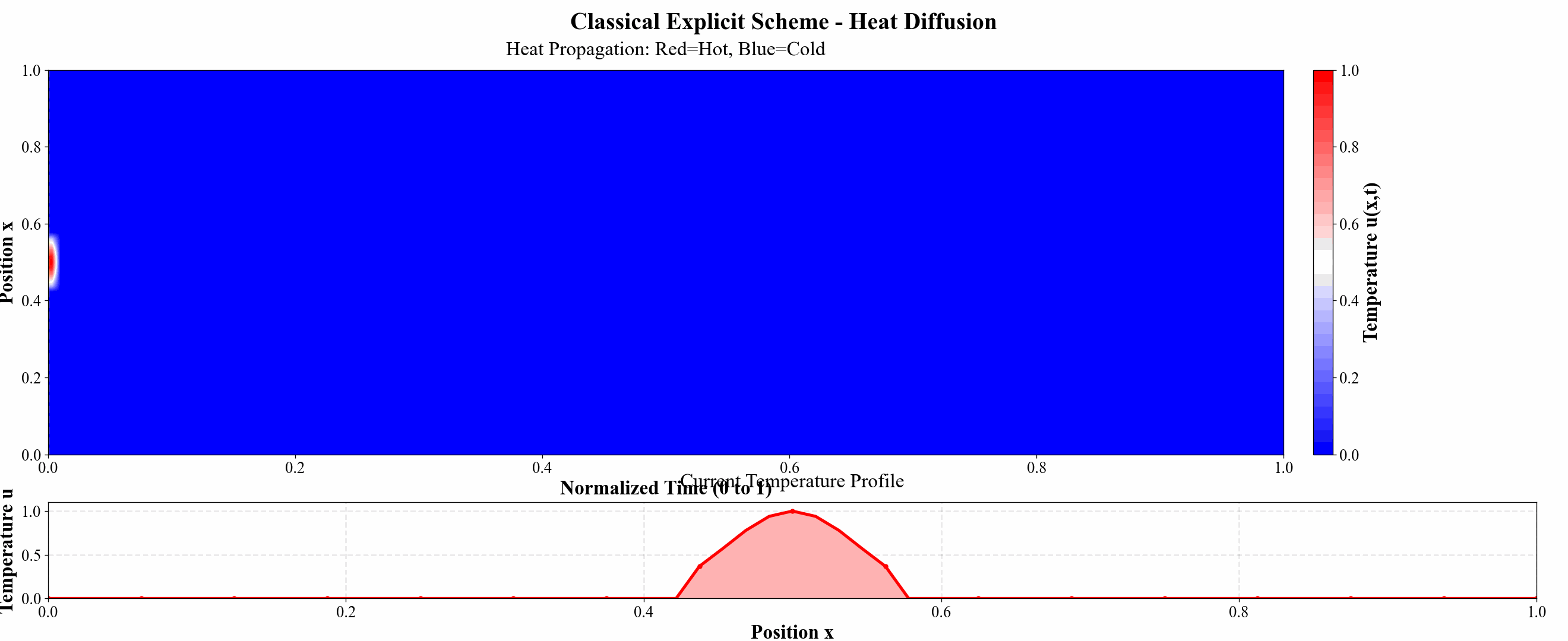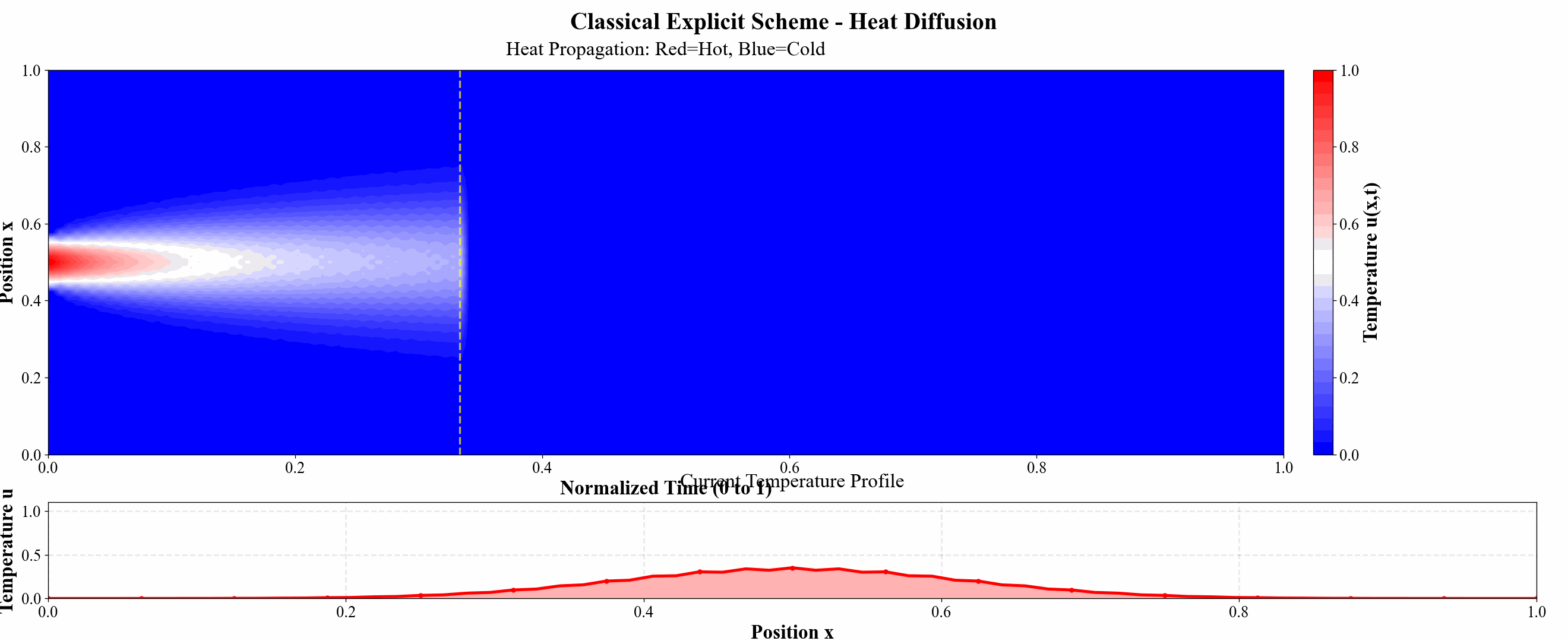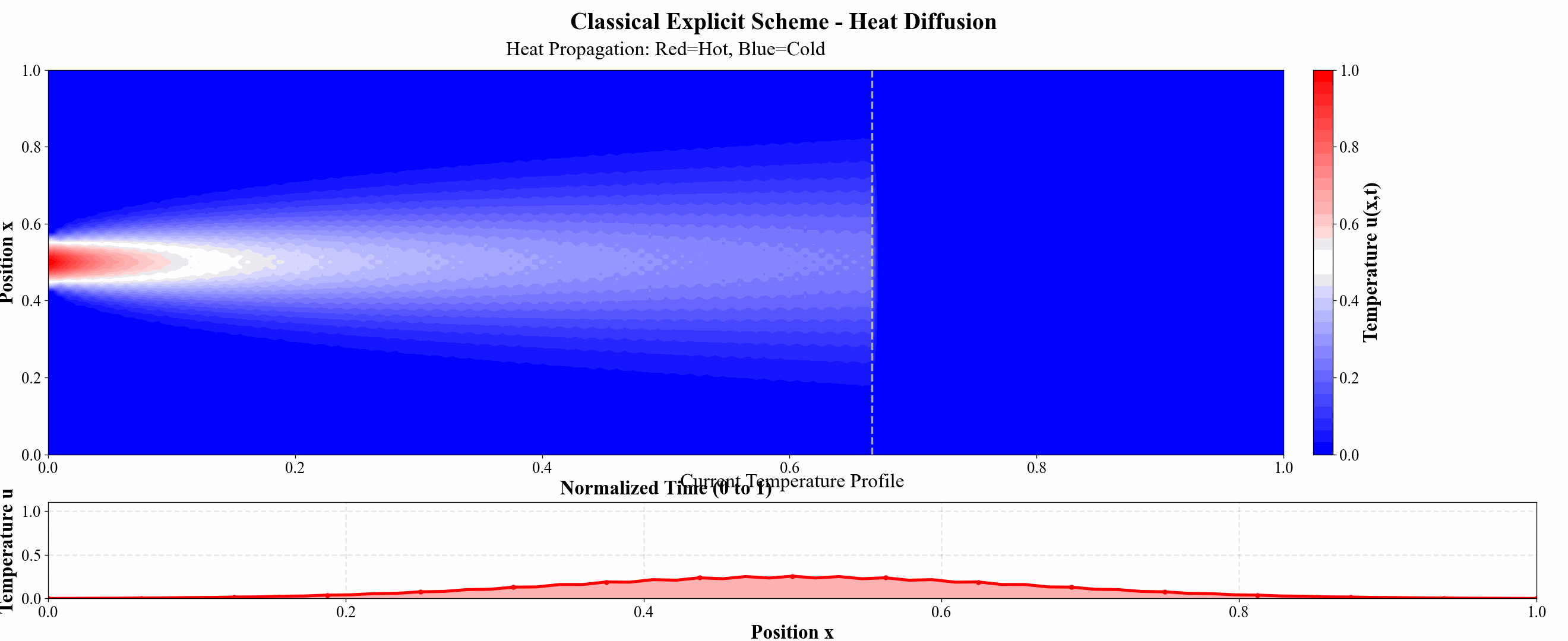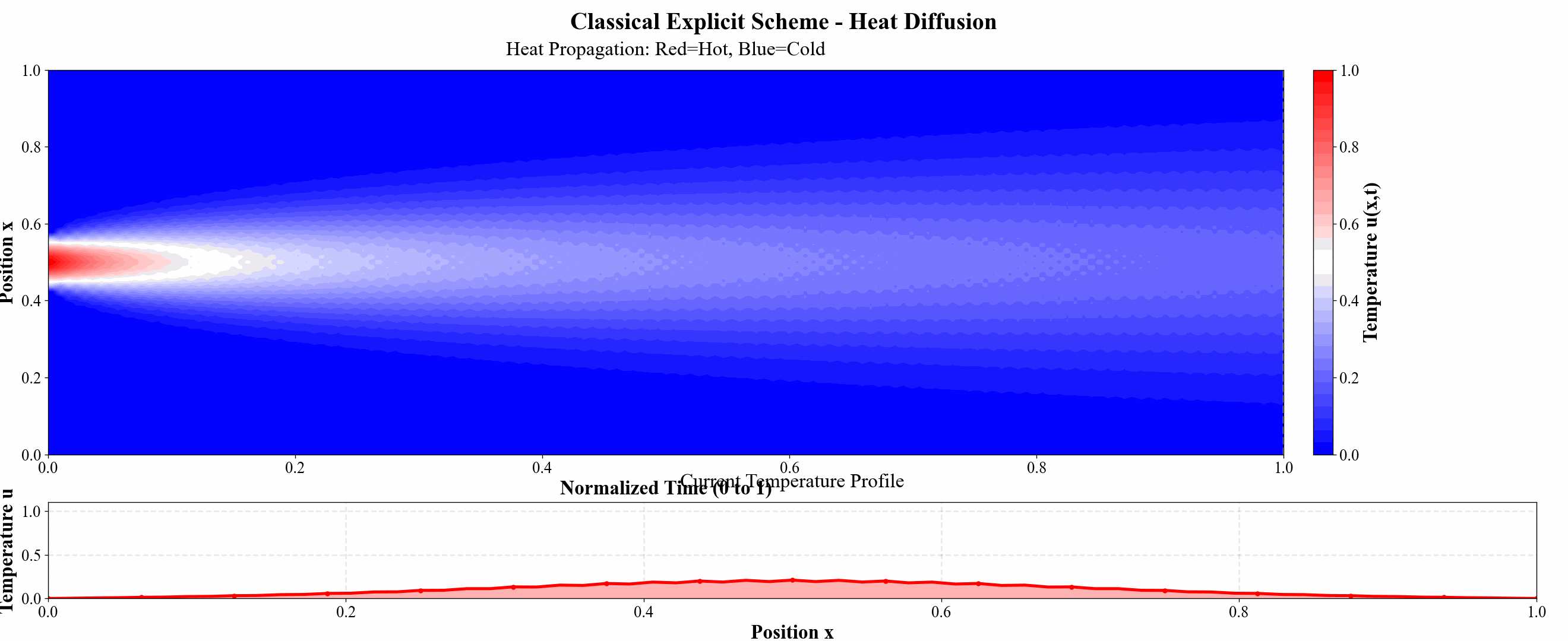
图 9 显式格式热力图
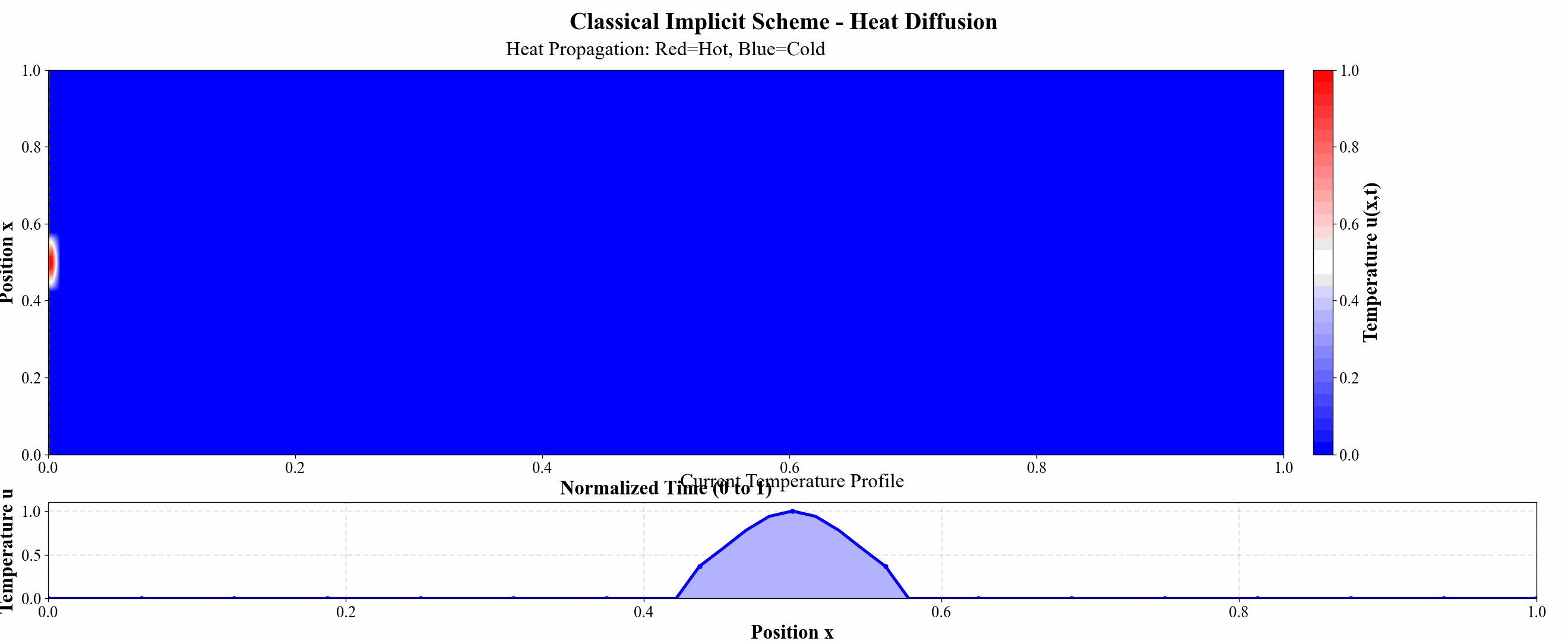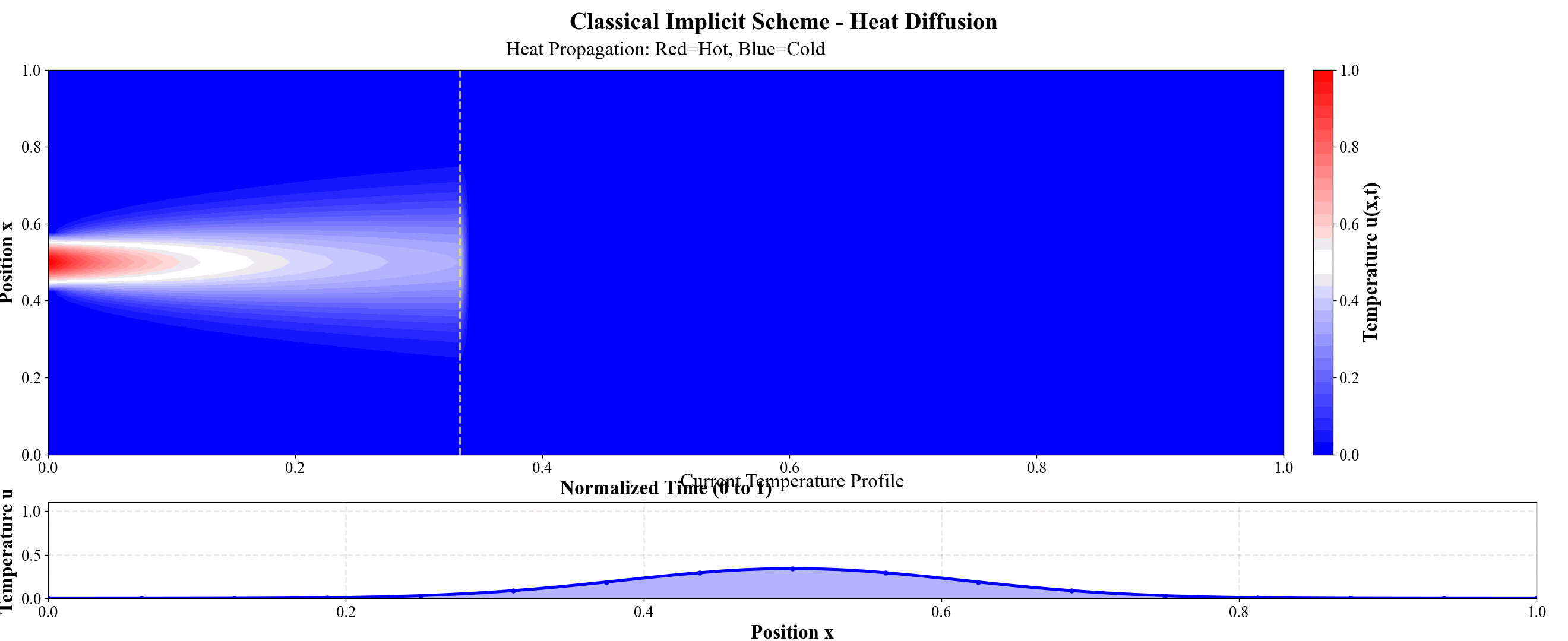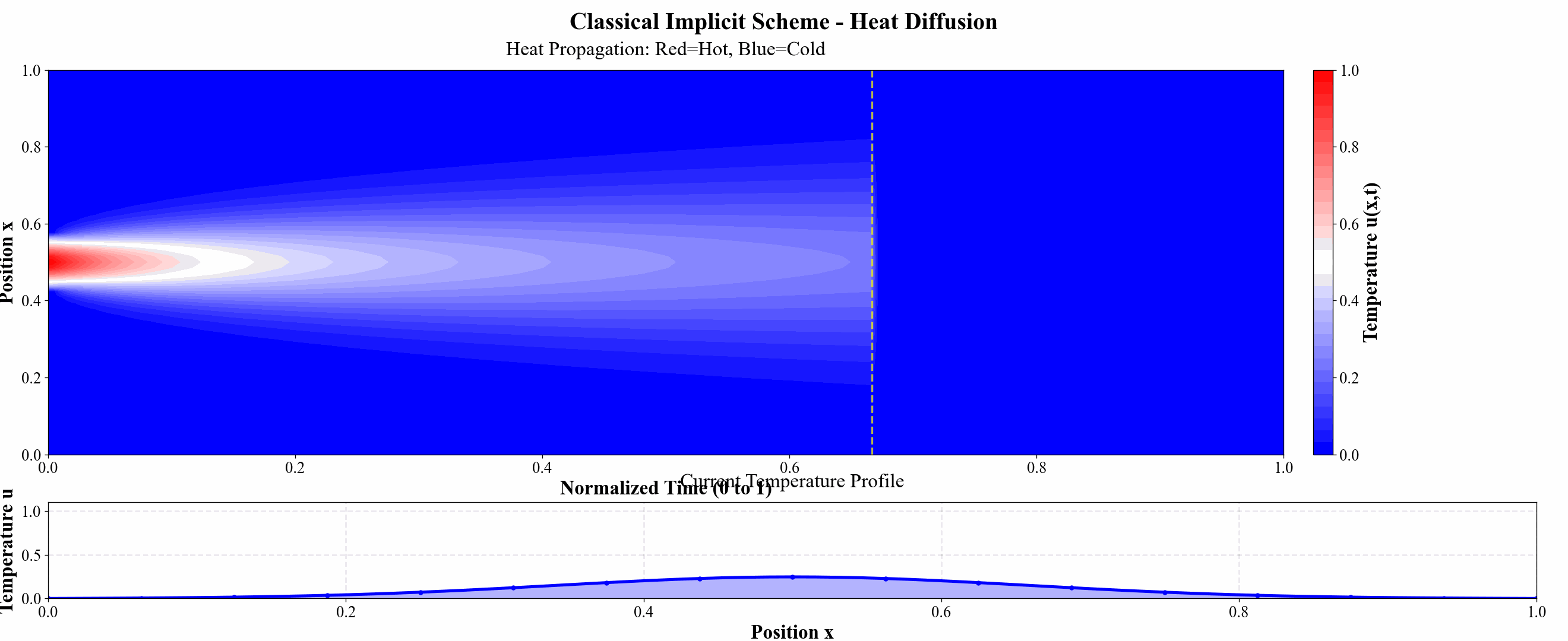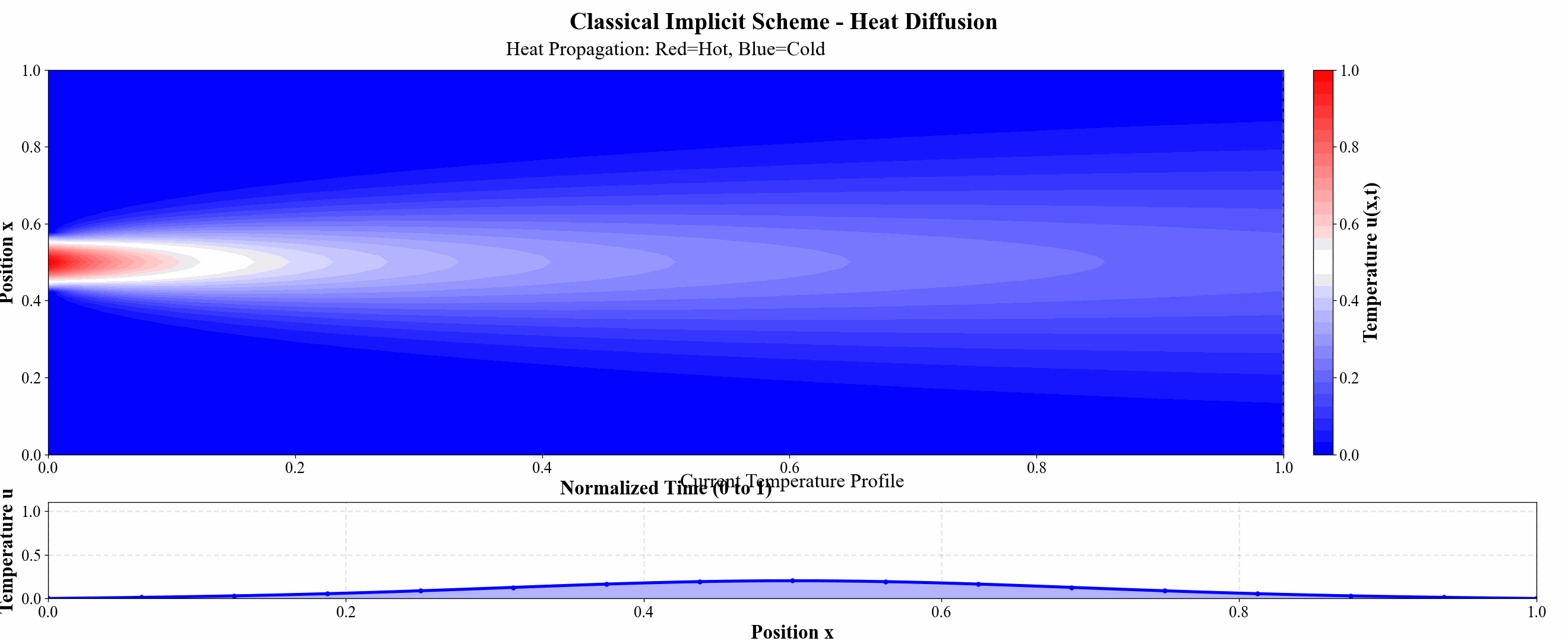
图 10 隐式格式热力图
图 11 Crank–Nicolson 格式热力图
计算中...